Tập tin:DragonCurve animation.gif
Từ testwiki
Bước tới điều hướng
Bước tới tìm kiếm
DragonCurve_animation.gif (641×480 điểm ảnh, kích thước tập tin: 143 kB, kiểu MIME: image/gif, có lặp, 29 khung ảnh, 17 s)
Tập tin này được lưu ở Wikimedia Commons và nó có thể được sử dụng ở các dự án khác. Lời miêu tả của tập tin tại trang mô tả được hiển thị dưới đây.
Miêu tả
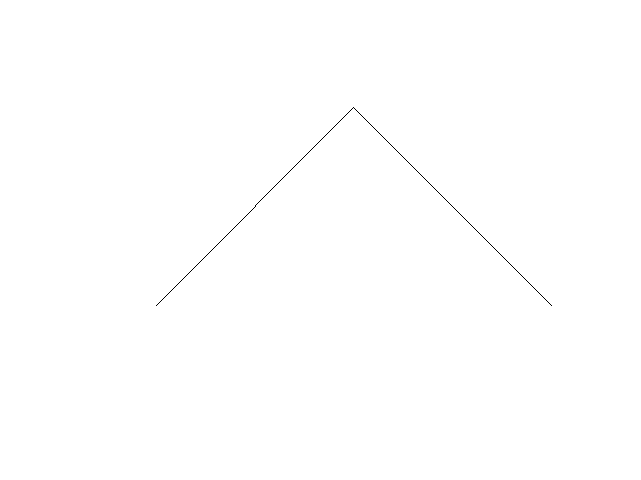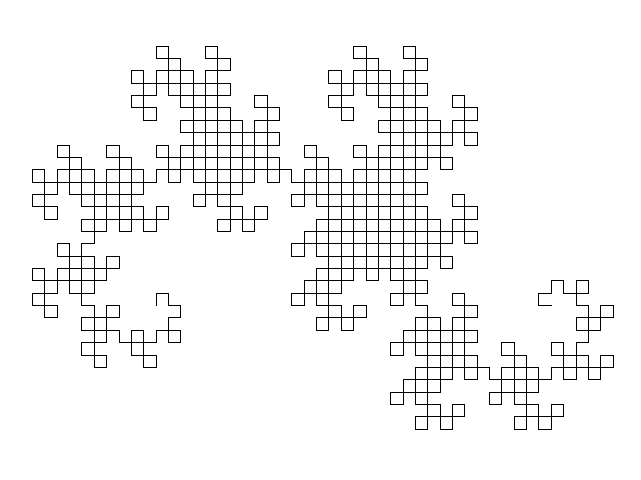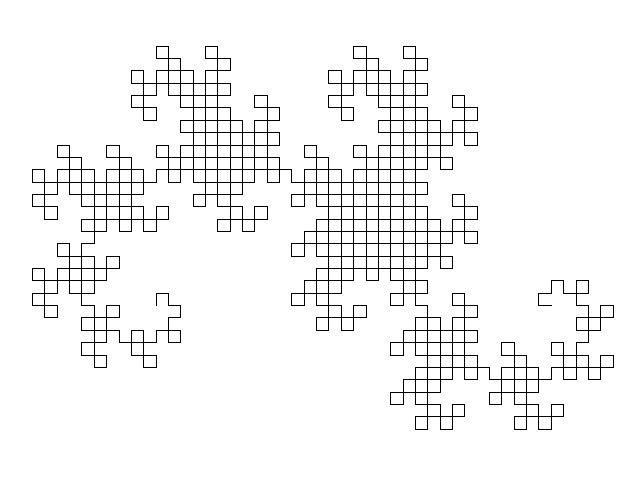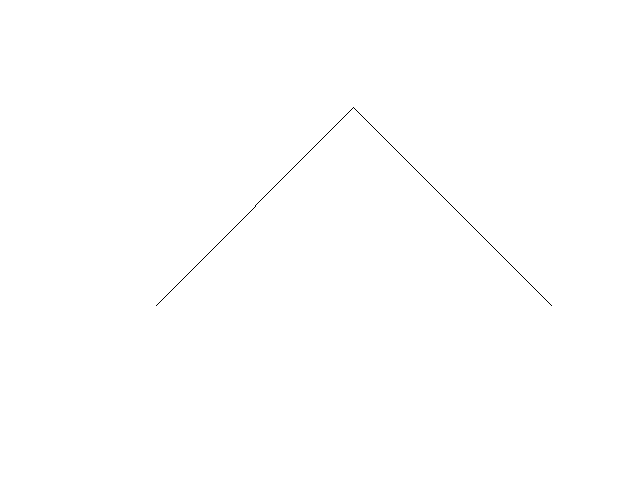
| Miêu tảDragonCurve animation.gif |
Français : Construction de la courbe du dragon English: Dragon curve construction |
| Ngày | |
| Nguồn gốc | Tác phẩm được tạo bởi người tải lên |
| Tác giả | Guillaume Jacquenot |
Source code (MATLAB)
function S = DragonCurve(pattern,MaxRecursionLevel)
% DRAGONCURVE
% This function generates a fractal curve called the dragon curve.
%
% A dragon curve is any member of a family of self-similar fractal curves,
% which can be approximated by recursive methods such as Lindenmayer
% systems.
%
% Inputs :
% - pattern : [Optional] Vector of complex that contain linear
% transformation to apply to each line segment
% - MaxRecursionLevel : [Optional] Maximum recusrion level
% Remember each time a new level is added, the
% number of line segments is doubled
% - options : [Optional] Structure with display option
%
% Outputs :
% - S : Structure that contains the line segment for each recursion level
% Just enter "plot(S(end).LineSeg,'k');" to plot the finest level
% generated
%
% See http://en.wikipedia.org/wiki/Dragon_curve
%
% 2011/07/10
% Guillaume Jacquenot
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if nargin < 3
options.plot = true;
options.generateGIFAnimate = true;
options.plotConvergence = false;
if nargin < 2
MaxRecursionLevel = 15;
if nargin < 1
pattern(1) = 0.5 * (1+1i);
pattern(2) = 0.5 * (1-1i);
end
end
end
S(MaxRecursionLevel) = struct('LineSeg',[]);
npat = numel(pattern);
S(1).LineSeg = [0;pattern(1:(npat-1));1];
for level = 2:MaxRecursionLevel;
delta = diff(S(level-1).LineSeg);
S(level).LineSeg = zeros(npat^level+1,1);
S(level).LineSeg(1:npat:end) = S(level-1).LineSeg;
S(level).LineSeg(2:4:end-3) = ...
S(level-1).LineSeg(1:2:end-2) + delta(1:2:end-1) * pattern(1);
S(level).LineSeg(4:4:end-1) = ...
S(level-1).LineSeg(2:2:end-1) + delta(2:2:end ) * pattern(2);
end
if options.plot || options.generateGIFAnimate
BBox = determineBoundingBox(S);
plotDragonCurve(S,BBox);
end
if options.generateGIFAnimate
cmd = generateGIFAnimationCommand(MaxRecursionLevel);
eval(cmd);
end
if options.plotConvergence
plot_Convergence_Evolution(S);
end
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plotDragonCurve(S,BBox)
figure('Color','w');
hold on
box on
axis off
MaxRecursionLevel = numel(S);
for level=1:MaxRecursionLevel
hp=plot(S(level).LineSeg,'k');
axis equal
axis(BBox);
saveas(gcf,[mfilename '_' sprintf('%03d',level)],'png');
saveas(gcf,[mfilename '_' sprintf('%03d',level)],'jpg');
plot2svg([mfilename '_' sprintf('%03d',level) '.svg']);
pause(0.5);
delete(hp);
end
plot(S(end).LineSeg,'k');
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function BBox = determineBoundingBox(S,proportionalOffset)
if nargin==1
proportionalOffset = 0.1;
end
BBox = zeros(1,4);
BBox(1) = min(real(S(end).LineSeg));
BBox(2) = max(real(S(end).LineSeg));
BBox(3) = min(imag(S(end).LineSeg));
BBox(4) = max(imag(S(end).LineSeg));
dBBoxX = BBox(2)-BBox(1);
dBBoxY = BBox(4)-BBox(3);
BBox = BBox + proportionalOffset * [-dBBoxX dBBoxX -dBBoxY dBBoxY];
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plot_Convergence_Evolution(S)
figure
hold on
box on
title('Evolution of the length of the curve with the number of levels');
xlabel('Level');
ylabel('Log of the length');
MaxRecursionLevel = numel(S);
lengthCurve = zeros(1,MaxRecursionLevel);
for level=1:MaxRecursionLevel
lengthCurve(level) = sum(abs(diff(S(level).LineSeg)));
end
plot(log2(lengthCurve));
grid on
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function cmd = generateGIFAnimationCommand(MaxRecursionLevel)
cmd = '!convert -antialias -density 100 -delay 60 ';
for level =[1:1:MaxRecursionLevel MaxRecursionLevel-1:-1:1]
cmd = [cmd mfilename '_' sprintf('%03d',level) '.png '];
end
cmd = [cmd mfilename '.gif'];
return;
Giấy phép
Tôi, người giữ bản quyền tác phẩm này, từ đây phát hành nó theo giấy phép sau:
Tập tin này được phát hành theo Giấy phép Creative Commons Ghi công - Chia sẻ tương tự 3.0 Chưa chuyển đồi
- Bạn được phép:
- chia sẻ – sao chép, phân phối và chuyển giao tác phẩm
- pha trộn – để chuyển thể tác phẩm
- Theo các điều kiện sau:
- ghi công – Bạn phải ghi lại tác giả và nguồn, liên kết đến giấy phép, và các thay đổi đã được thực hiện, nếu có. Bạn có thể làm các điều trên bằng bất kỳ cách hợp lý nào, miễn sao không ám chỉ rằng người cho giấy phép ủng hộ bạn hay việc sử dụng của bạn.
- chia sẻ tương tự – Nếu bạn biến tấu, biến đổi, hoặc tạo tác phẩm mới dựa trên tác phẩm này, bạn chỉ được phép phân phối tác phẩm mới theo giấy phép y hệt hoặc tương thích với tác phẩm gốc.
Chú thích
Ghi một dòng giải thích những gì có trong tập tin này
Khoản mục được tả trong tập tin này
mô tả
Giá trị nào đó không có khoản mục Wikidata
10 7 2011
image/gif
Lịch sử tập tin
Nhấn vào ngày/giờ để xem nội dung tập tin tại thời điểm đó.
| Ngày/Giờ | Hình xem trước | Kích cỡ | Thành viên | Miêu tả | |
|---|---|---|---|---|---|
| hiện tại | 21:57, ngày 10 tháng 7 năm 2011 |  | 641×480 (143 kB) | wikimediacommons>Gjacquenot | Reduce resolution |
Trang sử dụng tập tin
Trang sau sử dụng tập tin này: