Đạo hàm của các hàm lượng giác

Bản mẫu:Lượng giác Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).

Biết được đạo hàm của sin(x) và cos(x), chúng ta dễ dàng tìm được đạo hàm của các hàm lượng giác còn lại do chúng được biểu diễn bằng hai hàm trên, bằng cách dùng quy tắc thương. Phép chứng minh đạo hàm của sin(x) và cos(x) được diễn giải ở bên dưới, và từ đó cho phép tính đạo hàm của các hàm lương giác khác. Việc tính đạo hàm của hàm lượng giác ngược và một số hàm lượng giác thông dụng khác cũng được trình bày ở bên dưới.

Đạo hàm của các hàm lượng giác và các hàm lượng giác ngược

$(\sin (x))=\cos (x)$

$(\cos (x))=-\sin (x)$

$(\tan (x))=\left(\frac{\sin (x)}{\cos (x)}\right)=\frac{{\cos }^2(x)+{\sin }^2(x)}{{\cos }^2(x)}=\frac{1}{{\cos }^2(x)}={\sec }^2(x)$

$(\cot (x))=\left(\frac{\cos (x)}{\sin (x)}\right)=\frac{-{\sin }^2(x)-{\cos }^2(x)}{{\sin }^2(x)}=-(1+{\cot }^2(x))=-{\csc }^2(x)$

$(\sec (x))=\left(\frac{1}{\cos (x)}\right)=\frac{\sin (x)}{{\cos }^2(x)}=\frac{1}{\cos (x)}.\frac{\sin (x)}{\cos (x)}=\sec (x)\tan (x)$

$(\csc (x))=\left(\frac{1}{\sin (x)}\right)=-\frac{\cos (x)}{{\sin }^2(x)}=-\frac{1}{\sin (x)}.\frac{\cos (x)}{\sin (x)}=-\csc (x)\cot (x)$

$(\arcsin (x))=\frac{1}{\sqrt{1-x^2}}$

$(\arccos (x))=\frac{-1}{\sqrt{1-x^2}}$

$(\arctan (x))=\frac{1}{x^2+1}$

$\begin{array}{cc}& ({\sec }^{-1}x{)}^{\prime }=\frac{1}{\left|x\right|\sqrt{x^2-1}}\\ & ({\csc }^{-1}x{)}^{\prime }=\frac{-1}{\left|x\right|\sqrt{x^2-1}}\\ & ({\mathrm{arccot}}^{-1}x{)}^{\prime }=\frac{-1}{1+x^2}\\ \end{array}$

Chứng minh đạo hàm của hàm sin và cos

Giới hạn của $\frac{\sin \theta }{\theta }$ khi θ → 0

Đường tròn tâm O bán kính r

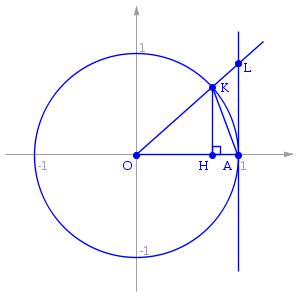
Cho đường tròn tâm O bán kính r (hình bên). Gọi θ là góc tại O tạo bởi OA và OK. Do ta giả định θ tiến dần tới 0, có thể xem θ là một số dương rất nhỏ: Bản mẫu:Nowrap.

Gọi: R₁ là diện tích tam giác OAK, R₂ là diện tích hình quạt OAK, R₃ là diện tích tam giác OAL. Dễ thấy:

$(R_1)<(R_2)<(R_3).$

Dùng công thức lượng giác, tính được diện tích tam giác OAK là

$\frac{1}{2}\times ||OA||\times ||OK||\times \sin \theta =\frac{1}{2}{r}^2\sin \theta .$

Diện tích hình quạt OAK là $\frac{1}{2}{r}^2\theta$, còn diện tích tam giác OAL là

$\frac{1}{2}\times ||OA||\times ||AL||=\frac{1}{2}\times r\times r\tan \theta =\frac{1}{2}{r}^2\tan \theta .$

Từ đó ta có:

$(R_1)<R_2)<(R_3)⟺\frac{1}{2}{r}^2\sin \theta <\frac{1}{2}{r}^2\theta <\frac{1}{2}{r}^2\tan \theta .$

Vì Bản mẫu:Nowrap ta chia bất đẳng thức trên cho ½·r². Ngoài ra, vì Bản mẫu:Nowrap dẫn đến Bản mẫu:Nowrap, ta có thể chia bất đẳng thức cho sin(θ), từ đó:

$1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }⟹1>\frac{\sin \theta }{\theta }>\cos \theta .$

Theo định lý kẹp ta có

$\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1.$

Trong trường hợp θ là số âm rất nhỏ là tiến dần tới 0, tức là: Bản mẫu:Nowrap, sử dụng tính chất lẻ của hàm sin ta được:

$\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{\sin (-\theta )}{-\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{-\sin \theta }{-\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1.$

Và do đó:

$\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta }=1.$

Giới hạn của $\frac{\cos \theta -1}{\theta }$ khi θ → 0

Ta có

$\underset{\theta \to 0}{\lim }\left(\frac{\cos \theta -1}{\theta }\right)=\underset{\theta \to 0}{\lim }\left[\left(\frac{\cos \theta -1}{\theta }\right)\left(\frac{\cos \theta +1}{\cos \theta +1}\right)\right]=\underset{\theta \to 0}{\lim }\left(\frac{{\cos }^2\theta -1}{\theta (\cos \theta +1)}\right).$

Vì Bản mẫu:Nowrap nên Bản mẫu:Nowrap Do đó

$\underset{\theta \to 0}{\lim }\left(\frac{\cos \theta -1}{\theta }\right)=\underset{\theta \to 0}{\lim }\left(\frac{-{\sin }^2\theta }{\theta (\cos \theta +1)}\right)=\underset{\theta \to 0}{\lim }\left(\frac{-\sin \theta }{\theta }\right)\times \underset{\theta \to 0}{\lim }\left(\frac{\sin \theta }{\cos \theta +1}\right)=(-1)\times \frac{0}{2}=0.$

Đạo hàm của hàm sin

Theo định nghĩa đạo hàm:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =\underset{\delta \to 0}{\lim }\left(\frac{\sin (\theta +\delta )-\sin \theta }{\delta }\right).$

Dùng công thức biến đổi lượng giác Bản mẫu:Nowrap và hai giới hạn vừa chứng minh ở trên, ta được

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =\underset{\delta \to 0}{\lim }\left(\frac{\sin \theta \cos \delta +\sin \delta \cos \theta -\sin \theta }{\delta }\right)=\underset{\delta \to 0}{\lim }[(\frac{\sin \delta }{\delta }\cos \theta )+(\frac{\cos \delta -1}{\delta }\sin \theta )]=(1\times \cos \theta )+(0\times \sin \theta )=\cos \theta .$

Đạo hàm của hàm cos

Theo định nghĩa:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =\underset{\delta \to 0}{\lim }\left(\frac{\cos (\theta +\delta )-\cos \theta }{\delta }\right).$

Dùng công thức biến đổi lượng giác Bản mẫu:Nowrap và hai giới hạn vừa chứng minh ở trên, ta được

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =\underset{\delta \to 0}{\lim }\left(\frac{\cos \theta \cos \delta -\sin \theta \sin \delta -\cos \theta }{\delta }\right)=\underset{\delta \to 0}{\lim }[(\frac{\cos \delta -1}{\delta }\cos \theta )-(\frac{\sin \delta }{\delta }\sin \theta )]=(0\times \cos \theta )-(1\times \sin \theta )=-\sin \theta .$

Chứng minh đạo hàm của các hàm ngược

Đạo hàm của hàm arcsin

Cho

$y=\arcsin x$

Trong đó

$-\frac{\pi }{2}\le y\le \frac{\pi }{2}$

Thì ta có

$\sin y=x$

Dùng đạo hàm ẩn và giải dy/dx:

$\frac{d}{dx}\sin y=\frac{d}{dx}x$

$\frac{dy}{dx}\cos y=1$

Thế $\cos y=\sqrt{1-{\sin }^{2}y}$,

$\frac{dy}{dx}\sqrt{1-{\sin }^{2}y}=1$

Thế $x=\sin y$,

$\frac{dy}{dx}\sqrt{1-x^2}=1$

$\frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}}$

Đạo hàm của hàm arccos

Cho

$y=\arccos x$

Trong đó

$0\le y\le \pi$

Thì ta có

$\cos y=x$

Dùng đạo hàm ẩn và giải dy/dx:

$\frac{d}{dx}\cos y=\frac{d}{dx}x$

$-\frac{dy}{dx}\sin y=1$

Thế $\sin y=\sqrt{1-{\cos }^{2}y}$,

$-\frac{dy}{dx}\sqrt{1-{\cos }^{2}y}=1$

Thế $x=\cos y$,

$-\frac{dy}{dx}\sqrt{1-x^2}=1$

$\frac{dy}{dx}=-\frac{1}{\sqrt{1-x^2}}$

Đạo hàm của hàm arctang

Cho

$y=\arctan x$

Trong đó

$-\frac{\pi }{2}<y<\frac{\pi }{2}$

Thì ta có

$\tan y=x$

Dùng đạo hàm ẩn và giải dy/dx

$\frac{d}{dx}\tan y=\frac{d}{dx}x$

$\frac{dy}{dx}{\sec }^{2}y=1$

Thế $1+{\tan }^{2}y={\sec }^{2}y$,

$\frac{dy}{dx}(1+{\tan }^{2}y)=1$

Thế $x=\tan y$,

$\frac{dy}{dx}(1+x^2)=1$

$\frac{dy}{dx}=\frac{1}{1+x^2}$

Xem thêm

• Lượng giác
• Vi tích phân
• Đạo hàm và vi phân của hàm số