Diện tích hình tròn
Diện tích hình tròn là diện tích của một hình tròn. Công thức của diện tích hình tròn là với Bản mẫu:Mvar là bán kính. Ở đây, chữ cái Hy Lạp [[Pi|Bản mẫu:Pi]] đại diện cho hằng số tỉ lệ giữa chu vi và đường kính của một hình tròn bất kì, gần bằng 3.1416.
Lịch sử
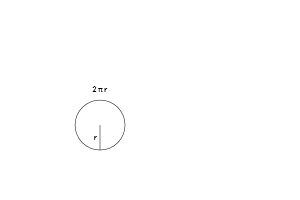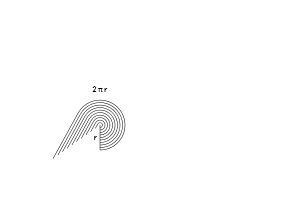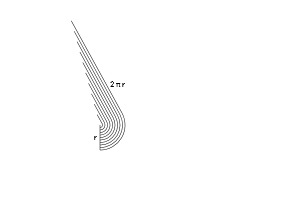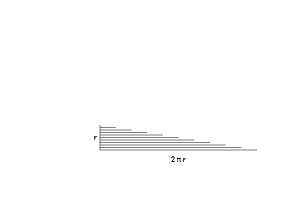
Diện tích của hình tròn đã được nghiên cứu bởi người Hy Lạp cổ đại. Eudoxus của Cnidus trong thế kỷ thứ 5 TCN đã tìm thấy rằng diện tích hình tròn là tỷ lệ thuận với bình phương bán kính của nó.[1] Archimedes sử dụng các công cụ của hình học Euclide thấy rằng diện tích một hình tròn là tương đương với một tam giác vuông với chiều dài bằng chu vi hình tròn và chiều cao bằng bán kính của hình tròn.
Sử dụng trong đa giác
Diện tích của một đa giác đều bằng một nửa chu vi của nó nhân với chiều dài đường trung đoạn của đa giác đều. Khi số lượng các cạnh của đa giác tăng lên, đa giác có xu hướng trở thành một hình tròn và các đường trung đoạn có xu hướng trở thành bán kính của hình tròn đó.[2]
Xem thêm
Tham khảo
Liên kết ngoài
- Area of a Circle Calculator Bản mẫu:Webarchive
- Area enclosed by a circle (with interactive animation)
- Science News on Tarski problem Bản mẫu:Webarchive
- Calculate disk area on fxSolver Bản mẫu:Webarchive
Bản mẫu:Toán học Bản mẫu:Sơ khai hình học
- ↑ Bản mẫu:Chú thích sách
- ↑ Hill, George. Lessons in Geometry: For the Use of Beginners, page 124 (1894).