Không gian thương (tô pô)

Hình cầu đồng phôi với không gian thương của một hình tròn, bằng cách dán tất cả các điểm biên của hình tròn với nhau thành một điểm.

$[0,1]/\{0,1\}$ đồng phôi với đường tròn $S^1$.

Trong tô pô và các ngành liên quan của toán học, không gian thương (quotient topology) của một không gian tô pô theo một quan hệ tương đương (hai ngôi) là một không gian tô pô mới, được xây dựng bằng cách gán tô pô thương cho tập hợp thương tương ứng, tức là tô pô mịn nhất sao cho các phép chiếu chuẩn tắc trở thành liên tục. Nói cách khác, một tập hợp trong không gian thương là mở khi và chỉ khi tạo ảnh của nó là mở trong không gian ban đầu.

Nói một cách trực quan, các điểm tương đương với nhau trong quan hệ tương đương sẽ được dính lại thành một điểm trong không gian thương. Ví dụ, nếu ta coi hai điểm đối xứng trên mặt cầu là tương đương với nhau, ta sẽ thu được một không gian thương là mặt phẳng xạ ảnh.

Định nghĩa

Cho $(X,{\tau }_X)$ là một không gian tô pô, và $\sim$ là một quan hệ tương đương trên $X$ $($nhắc lại, một quan hệ toán học 2 ngôi $\sim$ trên một tập $X$ là một tập con của $X\times X$, nghĩa là

$\sim$ $\subseteq X\times X$$)$. Tập hợp thương $Q=X/\sim$ là tập hợp gồm tất cả các lớp tương đương trên $X$ theo quan hệ $\sim$ . Thông thường, lớp tương đương của một phần tử $x\in X$ được ký hiệu là $[x]$, hoặc $\tilde{x}$, hoặc $\bar{x}$, nghĩa là:

$[x]=\{y\in X|y\sim x\}$     

$Q=(X/\sim )=\{[x]|x\in X\}$

• Không gian thương $Q$ được trang bị tô pô thương:

${\tau }_Q=\{U\subseteq Q|\{x\in X:[x]\in U\}\in {\tau }_X\}$

là tô pô mà các tập mở là các tập $U\subseteq Q$ thỏa mãn tập $\{x\in X:[x]\in U\}$ là mở trong $(X,{\tau }_X)$.

• Một cách tương đương, các tập mở của không gian thương $(Q,{\tau }_Q)$ là các tập $U\subseteq Q$ sao cho dưới toàn ánh

$f:(X,{\tau }_X)⟶(Q,{\tau }_Q)$

         $x⟼f(x)=[x]$

nghịch ảnh $f^{-1}\left(U\right)$ là mở trong $(X,{\tau }_X)$.

• Tô pô thương là tô pô cuối (final topology) của tập hợp thương theo ánh xạ $x⟼[x]$.

Ánh xạ thương (quotient map)

• Một ánh xạ $f:(X,{\tau }_X)⟶(X/\sim ,{\tau }_{X/\sim })$ được gọi là ánh xạ thương (identification map) nếu nó toàn ánh và $(U\in {\tau }_{X/\sim ,{\tau }_{X/\sim }}⟺f^{-1}(U)\in {\tau }_X)$.

Một cách tương đương, $f$ là ánh xạ thương $⟺$ $f$ toàn ánh và $X/\sim$ đươc trang bị tô pô cuối cùng theo $f$.

• Cho $(X,{\tau }_X)$ là một không gian tô pô với quan hệ tương đương $\sim$ . Khi đó ánh xạ chính tắc (canonical map) $q:(X,{\tau }_X)⟶(X/\sim ,{\tau }_{X/\sim })$ là một ánh xạ thương.

Ví dụ

• Phép dán (gluing). Các nhà tô pô học thường nói về việc dán các điểm lại với nhau. Cho không gian tô pô $(X,{\tau }_X)$, dán 2 điểm $x,y$ trong $X$ có nghĩa là ta xét không gian thương thu được từ quan hệ tương đương $a\sim b\iff a=b$ hoặc $(a,b)=(x,y)$ hoặc $(a,b)=(y,x)$.
• Xét hình vuông đơn vị với quan hệ tương đương $\sim$ sinh bởi điều kiện tất cả các điểm biên đều tương đương, do đó ta lập được 1 lớp tương đương gồm tất cả điểm biên của $[0,1{]}^2$. Khi đó $([0,1{]}^2/\sim )\cong S^2$, với $S^2$ là một mặt cầu bất kỳ.

Ví Bản mẫu:Webarchive dụ, $[0,1]/\{0,1\}$ đồng phôi với đường tròn $S^1$

• Không gian mở rộng (adjunction space). Tổng quát, cho không gian tô pô$(X,{\tau }_X)$ và không gian con $(A,{\tau }_A)$ với ${\tau }_A=\{A\cap U|U\in {\tau }_X\}$. Ta có thể gộp tất cả phần tử của $A$ thành một lớp tương đương và tất cả các phần tử của $X\setminus A$ thành một lớp tương đương., nghĩa là

    $\mathrm{\forall }a\in A,[a]=A$

    $\mathrm{\forall }b\in X\setminus A,[b]=X\setminus A$

Khi đó, ta nhận được không gian thương được kí hiệu là $X/A$. Mặt cầu 2 chiều đồng phôi với một hình tròn đóng, với biên được xác định bởi đúng một điểm: $D^2/\partial D^2$.

• Xét không gian $ℝ$ với tô pô Euclide, với quan hệ tương đương $x\sim y\iff (x-y)\in \mathbb{Z}$. Khi đó $ℝ/\sim$ đồng phôi với đường tròn đơn vị $S^1$ qua phép đồng phôi $[x]⟼e^{\frac{2\pi }{x}}$.
• Tổng quát hóa của ví dụ trước: cho $(G,\cdot ,{\tau }_G)$ là một nhóm tô pô tác động liên tục lên không gian tô pô $(X,{\tau }_X)$. Xét quan hệ tương đương trong $X$ bởi $x\sim y\iff \mathrm{\exists }z\in G:x,y\in {𝒪}_z$, với ${𝒪}_z=G\cdot z=\{g\cdot z|g\in G\}$ là quỹ đạo của $z$ bởi tác động liên tục của $G$ lên tập hợp tất cả nhóm con của $G$. Khi đó $X/\sim$ được gọi là không gian quỹ đạo (orbit space), kí hiệu là $X/G$. Trong ví dụ trước, $G=\mathbb{Z}$ tác động tịnh tiến lên $ℝ$. Không gian quỹ đạo $ℝ/\mathbb{Z}$ đồng phôi với $S^1$.

Ghi chú: $ℝ/\mathbb{Z}$ là một khái niệm vẫn còn mơ hồ. Nếu hiểu theo nghĩa $\mathbb{Z}$ là một nhóm với phép cộng tác động lên $ℝ$ thì không gian thương đồng phôi với đường tròn. Nếu hiểu theo nghĩa $\mathbb{Z}$ là một không gian con của $ℝ$ thì không gian thương đồng phôi với vô hạn đếm được cánh hoa giao nhau tại 1 điểm.

Tính chất

• Cho $(Y,{\tau }_Y)$ là một không gian thương của $(X,{\tau }_X)$. Ánh xạ thương $q:(X,{\tau }_X)⟶(Y,{\tau }_Y)$, là đặc trưng trong các toàn ánh do tính chất sau:

Sơ đồ hợp nối ánh xạ giữa các không gian $X,Y$ và $Z$

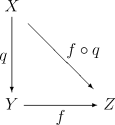
cho không gian tô pô $(Z,{\tau }_Z)$ và $f:(Y,{\tau }_Y)⟶(Z,{\tau }_Z)$, khi đó $f$ liên tục $⟺$$f\circ q$ liên tục.

• Không gian thương $X/\sim$ cùng với ánh xạ thương $q:X⟶X/\sim$ được đặc trưng bởi tính phổ dụng (universal property) : nếu ánh xạ$g:(X,{\tau }_X)⟶(Z,{\tau }_Z)$ là liên tục và thỏa mãn $g(a)=g(b),\mathrm{\forall }a,b\in X:a\sim b$, thì khi đó $\mathrm{\exists }$ $!$ $f:(X/\sim ,{\tau }_{X/\sim })⟶(Z,{\tau }_Z)$ sao cho $g=f\circ q$. Ta nói $g$ là một ánh xạ hạn chế thương. Do đó, các ánh xạ liên tục được xác định trên $X/\sim$ chính là các ánh xạ được sinh bởi các ánh xạ liên tục được xác định trên $X$ theo quan hệ tương đương (theo nghĩa là chúng gửi các phần tử tương đương vào cùng một tạo ảnh). Tiêu chí này được sử dụng nhiều khi nghiên cứu không gian thương.
• Cho toàn ánh liên tục $q:X⟶X/\sim$. Ta có thể đặt câu hỏi với điều kiện nào thì $q$ là một ánh xạ thương ? Điều kiện đủ là $q$ là ánh xạ mở (điều này tương đương với $q$ là ánh xạ đóng). Lưu ý rằng đây là điều kiện đủ chứ không phải điều kiện cần (nhắc lại: cho 2 mệnh đề P và Q, nếu P đúng $\Rightarrow$ Q đúng thì P là điều kiện đủ của Q và Q là điều kiện cần của P) Ta có thể dễ dàng xây dựng các ví dụ về ánh xạ thương mà không phải là ánh xạ mở. Đối với các nhóm tô pô, ánh xạ thương là ánh xạ mở.

Tương quan với các khái niệm tô pô khác

Sự tách (separation)

• Nói chung, hệ tiên đề tách là không đúng đối với các không gian thương. Không gian thương $X/\sim$ không nhất thiết kế thừa các tính chất tách của $X$, và $X/\sim$ có thể có những tính chất tách mà $X$ không có.
• $X/\sim$ là không gian $T_1$ $⟺$ mọi lớp tương đương là đóng trong $X$.
• Nếu ánh xạ thương là ánh xạ mở, thì $X/\sim$ là Hausdorff $⟺$ $\sim$ là một tập con đóng trong không gian tích $(X\times X,\rho )$ với $\rho$ là tô pô tích (nhác lại, một quan hệ toán học 2 ngôi $\sim$ trên một tập $X$ là một tập con của $X\times X$, nghĩa là $\sim$ $\subseteq X\times X$).

Tính liên thông (connectedness)

• Nếu một không gian là liên thông (hoặc liên thông đường) thì mọi không gian thương của nó cũng liên thông (hoặc liên thông đường)
• Nếu một không gian là đơn liên (hoặc co rót được-contractible space) thì không gian thương của nó không nhất thiết có các tính chất đó.

Tính compact

• Nếu một không gian là compact thì mọi không gian thương của nó cũng compact.
• Nếu một không gian là compact địa phương thì không gian thương của nó không nhất thiết compact địa phương.

Số chiều (Dimension)

• Số chiều tô pô của một không gian thương có thể lớn hơn hoặc bé hơn số chiều của không gian ban đầu. Đường cong phủ không gian cho ta các ví dụ như vậy.

Thư mục

• Bản mẫu:Chú thích sách

Liên kết ngoài

• Bản mẫu:Planetmath reference
• Không gian thương Bản mẫu:Webarchive tại omarine

Đọc thêm

• Bản mẫu:Chú thích sách
• Bản mẫu:Chú thích sách